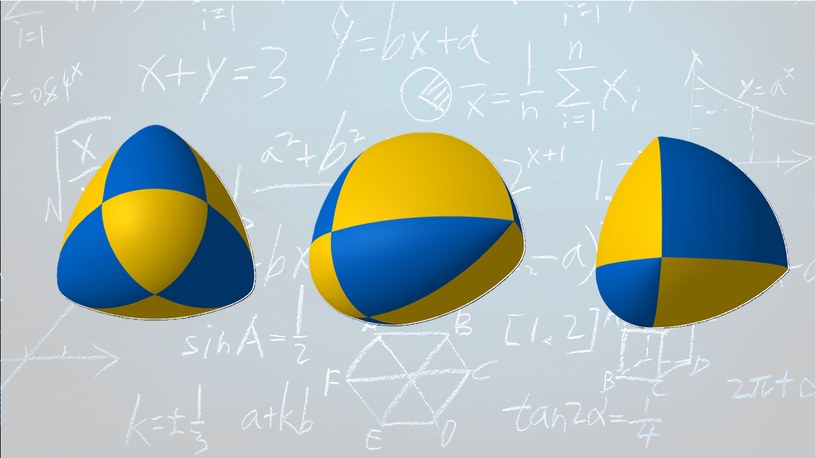
Dla przeciętnego człowieka, który ma kontakt z podstawową matematyką 2+2 zawsze będzie dawało 4. Mamy koło, kwadrat i inne figury geometryczne, co tu więcej wymyślić. No ok, zawsze możemy narysować jakiś niespotykany, wymyślny kształt. Ale czy to znaczy, że od razu jesteśmy odkrywcami na miarę Nobla (pomijając fakt, że w dziedzinie matematyki tej nagrody się nie przyznaje)? Poznajcie sami najnowsze odkrycie królowej nauk, a zobaczycie, w czym tkwi sekret.
Matematycy tworzą nowe kształty i figury
Nowa figura geometryczna na pierwszy rzut oka w dwóch wymiarach przypomina lub: trójkąt równoboczny z zakrzywionymi łukami łączącymi się w narożnikach. Tworzy kształt o stałej szerokości i powierzchni mniejszej niż okrąg. Zespół matematyków poinformował, że dodał do niego trzeci wymiar, co rozwiązało. Wówczas w matematyk Oded Schramm prowadził rozważania, czy mogą istnieć obiekty o stałej szerokości mniejszej niż kula o większym wymiarze.
Jak poinformował New Scientist nowo odkryty kształt będzie proporcjonalnie mniejszy niż kula o równoważnym wymiarze. Może się również toczyć się równie płynnie, co koło, nawet jeśli nie jest okrągły. Odkrycie zostało przedstawione na… gdzie zarejestrowani autorzy mogą dodać prace nierecenzowane i nieopublikowane w czasopiśmie naukowym.
Nowe wyzwania dla matematyków
Teraz matematykom czeka nie mniejsze wyzwanie, a mianowicie. W marcu 2023 roku mogliście o wysiłkach, które miały na celu wymyślenie „einsteina”, wyjątkowego kształtu, pozwalającego stworzyć absolutnie niepowtarzalną mozaikę. Co ciekawe w przypadku tej nazwy i gry słów wcale nie chodzi o słynnego naukowca, ale o wykorzystanie jednego kształtu, jednej płytki. „Einstein” z j. niemieckiego możemy przetłumaczyć jako „jeden kamień”.
Udało się, tak powstał (niektórzy upatrywali raczej koszulę z krótkim rękawem), czyli kształt, który ma 13 boków. Ale aby ułożyć niepowtarzalny wzór, trzeba było zastosować „kapelusze” oraz ich lustrzane odbicia. Później ci sami naukowcy wprowadzili modyfikacje w swoim wzorze, dzięki czemu stworzyli „widmo” nazwane następnie. Ulepszony kształt można ułożyć bez stosowania lustrzanego odbicia. Natomiast sama nazwa jest oczywiście nawiązaniem do humanoidalnych krwiopijców, którzy nie mogą przejrzeć się w lustrze.
Zastosowania matematycznych kształtów
Po co matematycy tworzą takie kształty? Już po opublikowaniu głosnego kapelusza matematycy znaleźli dla niego niezwykle ważne zastosowanie. Świetnie nadaje się do zastosowania… na płytkach podłogowych dla kogoś, kto chce mieć niepowtarzalny wzór. Stał się także dużą inspiracją dla artystów. To oczywiście nie koniec, z punktu widzenia inżynierii, takie kształty również mogą znaleźć zastosowanie, jak np..
Nie jest to żadną tajemnicą, że w przypadku nauk podstawowych często liczy się samo wynalezienie, opracowanie nowego kształtu, nowego wynalazku. Odkrycie jego zastosowania może przyjść dopiero z czasem. Z pewnością tak będzie i w tym przypadku. Coż, płytek z tego nie ułożymy, ale przyszło już lato, to może zaczniemy od fikuśnych piłek plażowych?